Quand on compare les statistiques concernant deux groupes différents (par exemple deux catégories de la population : vaccinés/non vaccinés), il faut faire attention à savoir si leurs caractéristiques ne sont pas trop éloignées, pour ne pas interpréter les résultats de manière erronée. Lucas Benjamin, Unsplash, CC BY
Auteurs
- Quentin BergerMaître de conférence, Sorbonne Université
- Francesco CaravennaFull Professor of Mathematics (Probability and Statistics), University of Milano-Bicocca
Reproduisez nos articles gratuitement, sur papier ou en ligne, en utilisant notre licence Creative Commons.
L’utilisation de statistiques peut être la source de résultats complètement contre-intuitifs, bien que démontrés rigoureusement. C’est ce que l’on appelle des paradoxes : un paradoxe n’est pas un résultat faux ou incompatible avec un autre résultat mais un résultat incompatible avec notre intuition.
Le paradoxe de Simpson
L’un des paradoxes de statistique les plus troublants est le paradoxe de Simpson, qui stipule qu’il est possible qu’un même phénomène ait lieu à l’intérieur de différents groupes, mais que ce phénomène s’inverse lorsque les groupes sont rassemblés. Il est à l’origine de nombreuses erreurs d’interprétations, même pour des mathématiciens aguerris.
En voici un exemple marquant, que nous avons trouvé dans les données d’hospitalisation et de vaccination en Angleterre.
Dans ces rapports, qui donnent les statuts de vaccinations des personnes hospitalisées du variant Delta du Covid entre juin et septembre 2021 (les données, les références complètes et les calculs sont donnés dans cet annexe), on observe que :
- parmi les moins de 50 ans, le taux de mortalité est environ 1,8 fois plus élevé chez les non-vaccinés que chez les vaccinés (ou partiellement vaccinés) ;
- parmi les plus de 50 ans, le taux de mortalité est environ 6,3 fois plus élevé chez les non-vaccinés que chez les vaccinés (ou partiellement vaccinés) ;
- par contre, dans la population prise dans son ensemble, le taux de mortalité est environ 1,3 fois moins élevé chez les non-vaccinés que chez les vaccinés (ou partiellement vaccinés).
Deux observations s’imposent. Premièrement, la dernière affirmation semble contredire les deux précédentes : comment expliquer que le vaccin abaisse le taux de mortalité à la fois parmi les plus de 50 ans et parmi les moins de 50 ans, mais l’augmente si l’on considère la population dans son ensemble ?
Deuxièmement (et de manière plus inquiétante), si l’on se base sur les moins de 50 ans et les plus de 50 ans séparément (c’est-à-dire si on regarde les points 1 et 2) ou si l’on considère la population prise dans son ensemble (c’est-à-dire si on regarde le point 3, sans différencier les plus ou moins de 50 ans), on aboutit à des conclusions complètement opposées quant à l’efficacité du vaccin. Plus précisément, si on regarde les points 1 et 2, le vaccin semble efficace pour réduire la mortalité, à la fois chez les moins de 50 ans et chez les plus de 50 ans. Tandis que si l’on considère la population dans son ensemble (c’est-à-dire le point 3), il paraît tout à fait légitime de conclure que le vaccin n’est pas du tout efficace, voire dangereux.
Explication du paradoxe
Les chiffres précis que l’on a donnés plus haut sont présentés en annexe, mais donnons ici une explication générale de la façon dont ce paradoxe peut se produire.
L’idée principale est que la proportion de personnes vaccinées est très différente chez les plus de 50 ans (environ 95 % sur la période juin-septembre d’après la NHS) et chez les moins de 50 ans (environ 50 % sur la période juin-septembre).
En effet, parmi les personnes non vaccinées, une grande proportion a moins de 50 ans et possède un taux de mortalité faible (en raison de leur âge). En revanche, parmi les personnes vaccinées une grande proportion a plus de 50 ans et possède un taux de mortalité plus élevé (même en étant vacciné). Cela explique que, dans la population totale, le taux de mortalité des non-vaccinés puisse être inférieur au taux de mortalité des vaccinés.
Voici une représentation visuelle où le paradoxe apparaît de manière claire, avec des données caricaturales pour rendre le phénomène plus apparent :
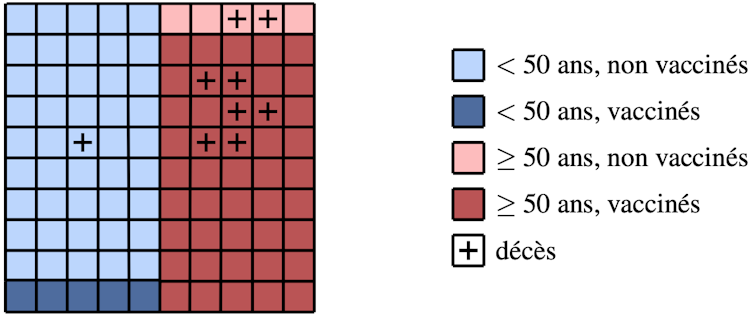
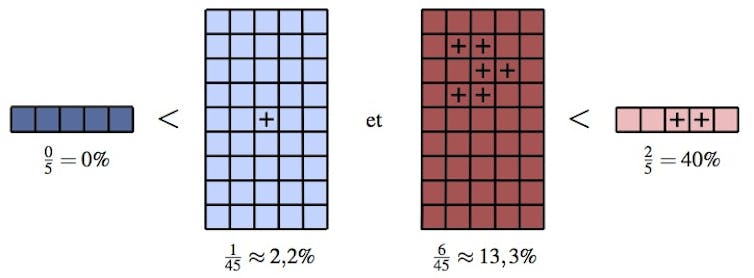
Si l’on considère les personnes de moins de 50 ans ou de plus de 50 ans comme deux groupes séparés, il est clair que les taux de mortalité sont moins élevés dans la population vaccinée :
Toutefois, si l’on considère la population dans son ensemble, le taux de mortalité devient plus élevé parmi les vaccinés que parmi les non-vaccinés, comme on le voit sur la figure suivante :
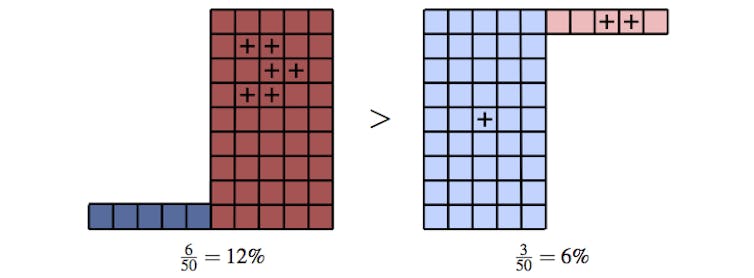
On voit que cela est dû au fait que parmi les personnes vaccinées, la plupart sont âgées de plus de 50 ans.
Quelles conclusions en tirer ?
Que conclure alors de ce paradoxe et de son explication ? Tout d’abord, qu’il faut prendre des précautions lorsque l’on manipule des statistiques et notamment lorsque l’on considère des groupes aux caractéristiques très différentes. En quelques mots, le paradoxe de Simpson tient dans le fait que le taux de vaccination est très variable d’une classe d’âge à l’autre : il est donc important de comparer l’efficacité du vaccin à l’intérieur de chaque classe d’âge, qui possède des caractéristiques plus homogènes.
Rassembler les différentes classes d’âge introduit ce que l’on appelle un « biais de sélection » : la population vaccinée est biaisée du côté de la population fragile (plus âgée) tandis que la population non vaccinée est biaisée du côté de la population moins fragile (plus jeune). Par conséquent, comparer le taux de mortalité chez les vaccinés et chez les non-vaccinés revient de facto à comparer une population plutôt âgée et une population plutôt jeune. L’affirmation que le taux de mortalité dans la population est plus élevé chez les vaccinés est donc foncièrement faussée par la grande variabilité du taux de vaccination pour les différentes tranches d’âge.
De la difficulté d’interpréter les statistiques
De façon plus générale, la problématique du biais de sélection est bien connue en statistique et fait partie des erreurs d’interprétation les plus courantes.
Un exemple classique est celui du statisticien Abraham Wald qui, durant la Seconde Guerre mondiale, après avoir observé tous les avions revenus du combat, recommanda de blinder les endroits où ceux-ci avaient été le moins touchés par des impacts de balles… Le raisonnement était que ces endroits constituaient les points les plus critiques pour le fonctionnement des avions et que ceux qui y étaient touchés avaient moins de chance de revenir du combat. Il s’agissait d’une manière de corriger ce qui est connu comme le « biais des survivants », qui consiste à faire des statistiques en ne conservant que les données de ceux qui survivent.
Les biais de sélection, qu’ils soient conscients ou non, font d’ailleurs souvent partie intégrante du procédé de récolte de données statistiques, ce qu’on voit bien dans l’exemple précédent. Il est important de savoir quels biais sont présents, pour corriger leur effet. Ainsi, le fait de comparer les taux de mortalité parmi les non-vaccinés et parmi les vaccinés comporte des biais d’âge, comme expliqué plus haut : une façon de corriger ce biais est de considérer les taux de mortalité pour les non-vaccinés et pour les vaccinés pour des tranches d’âge restreintes, à l’intérieur desquelles le taux de vaccination est stable.
Pour conclure, les paradoxes sont là pour nous rappeler, de manière particulièrement saisissante, les écueils à éviter. Grâce à leur côté surprenant, ils nous marquent et nous aident à aiguiser notre intuition, ou au moins à s’en méfier. Ils nous rappellent que personne n’est infaillible et qu’il n’est pas toujours facile ni immédiat de démêler certains problèmes, même simples : ils nous poussent à entraîner et approfondir notre réflexion, avec humilité.
Pour les amateurs de paradoxes, en voici quelques-uns parmi les plus classiques dans le domaine des probabilités : le paradoxe des anniversaires, le paradoxe de Bertrand, le problème de Monty Hall, le paradoxe des prisonniers, le paradoxe des enfants…



